Geometric Machine Learning

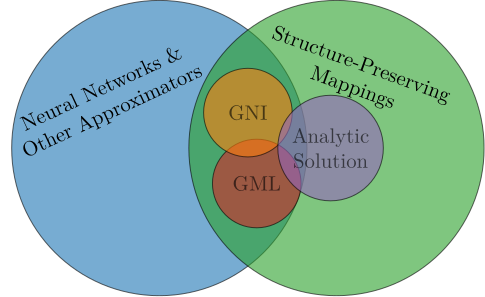
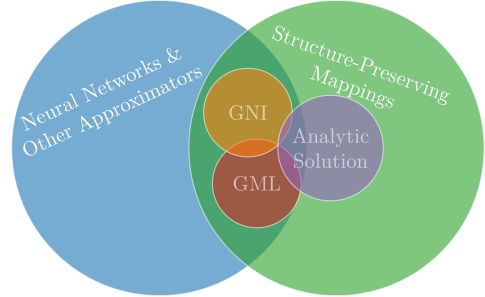
GeometricMachineLearning is a package for structure-preserving scientific machine learning. It contains models that can learn dynamical systems with geometric structure, such as Hamiltonian (symplectic) or Lagrangian (variational) systems.

In that regard its aim is similar to traditional geometric numerical integration [1, 2] in that it models maps that share properties with the analytic solution of a differential equation:

Installation

GeometricMachineLearning and all of its dependencies can be installed via the Julia REPL by typing

]add GeometricMachineLearning

Architectures

Some of the neural network architectures in GeometricMachineLearning [3, 4] have emerged in connection with developing this package^[1], other have existed before [5, 6].

New architectures include:

• symplectic autoencoder,
• volume-preserving transformers,
• linear-symplectic transformer.

Existing architectures include:

• SympNets,
• standard transormer.

Manifolds

GeometricMachineLearning supports putting neural network weights on manifolds such as the Stiefel manifold and the Grassmann manifold and Riemannian optimization.

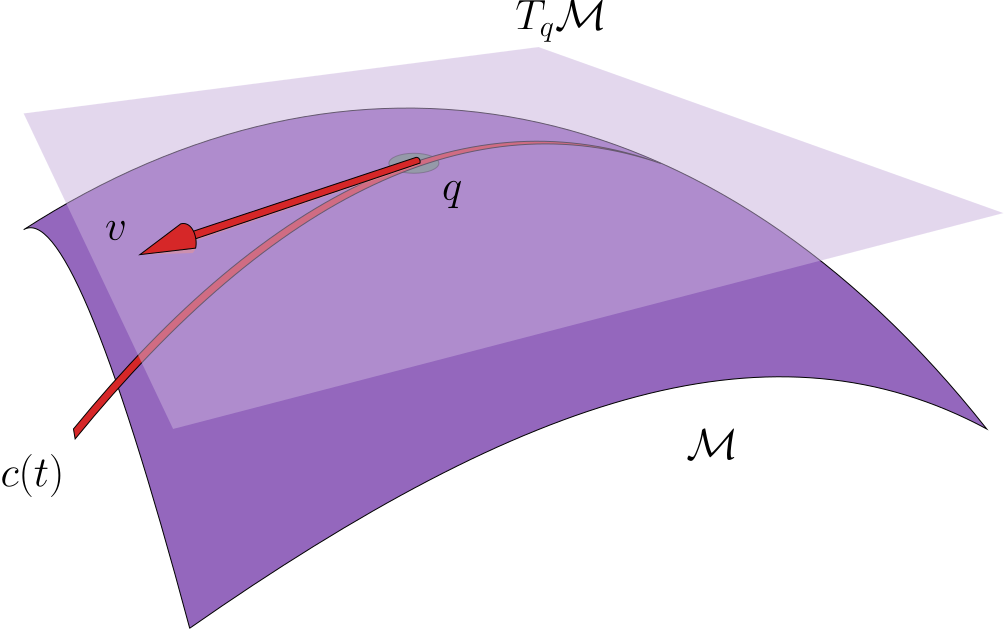
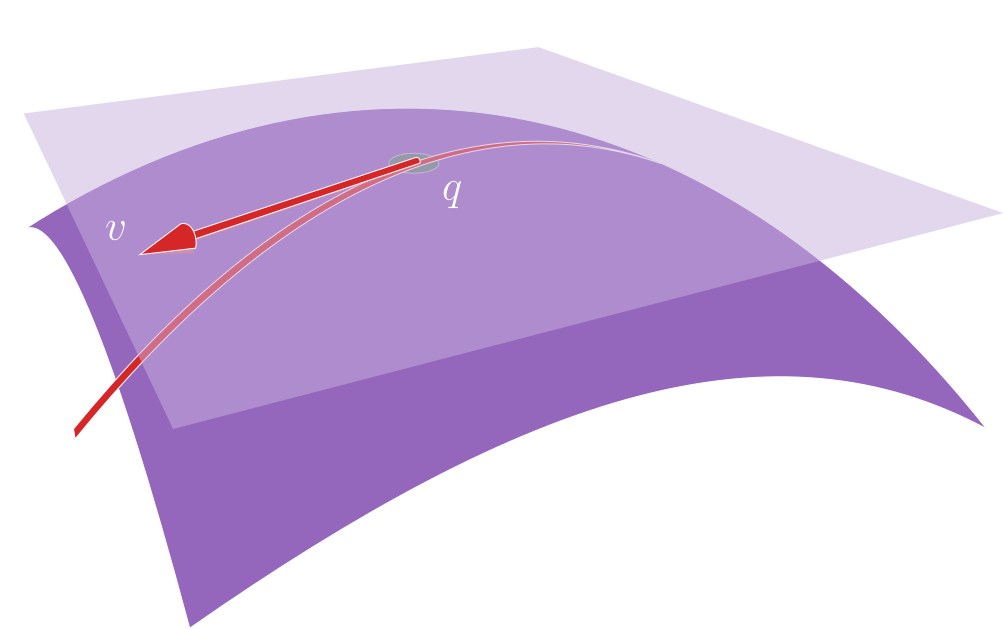
When GeometricMachineLearning optimizes on manifolds it uses the framework introduced in [7]. Optimization is necessary for some neural network architectures such as symplectic autoencoders and can be critical for others such as the standard transformer [8, 9].

Special Neural Network Layer

Many layers have been adapted in order to be used for problems in scientific machine learning, such as the attention layer.

GPU Support

All neural network layers and architectures that are implemented in GeometricMachineLearning have GPU support via the package KernelAbstractions.jl [10], so GeometricMachineLearning naturally integrates CUDA.jl [11], AMDGPU.jl, Metal.jl [12] and oneAPI.jl [13].

Tutorials

There are several tutorials demonstrating how GeometricMachineLearning can be used.

These tutorials include:

• a tutorial on SympNets that shows how we can model a flow map corresponding to data coming from an unknown canonical Hamiltonian system,
• a tutorial on symplectic Autoencoders that shows how this architecture can be used in structure-preserving reduced order modeling,
• a tutorial on the volume-preserving attention mechanism which serves as a basis for the volume-preserving transformer,
• a tutorial on training a transformer with manifold weights for image classification to show that manifold optimization is also useful outside of scientific machine learning.

Data-Driven Reduced Order Modeling

The main motivation behind developing GeometricMachineLearning is reduced order modeling, especially structure-preserving reduced order modeling. For this purpose we give a short introduction into this topic.